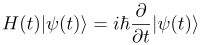Тема: Задачка для полутехников
выпускники "илитного" вуза считают себя умными, дак попробуйте решить
ну и просто тем кто хочет мозг напрячь, расшифруйте:
а анимированные гифки тут не работают?
тогда частями, упрощаем задачку:
Задача 2:
на сфере выбирают произвольно 4 точки, соединяют их так что получается фигура типа пирамиды,
какова вероятность что центр сферы попадёт внутрь этой фигуры? 😆
Задача 3: детская
5 станков за 5 минут делают 5 деталей, за какое время 100 станков выточат 100 деталей?
Задача 4: детская
набор шарик для пингпонга и ракетка стоит 1 рубль 10 копеек, при этом ракетка дороже шарика на 1 рубль,
сколько стоит шарик?
Задача 5: детская
количество тины на поверхности пруда удваивается каждый день, за 12 дней заросло половина пруда, за сколько зарастёт весь пруд?
Задача 6: школьная
дана окружность, как с помощью карандаша и угольника(без делений) найти центр окружности? отметки на угольнике делать нельзя
Задача 7: как и первая сомнительно что полутехники решат
Пусть f - функция с вещественными значениями, заданная на плоскости, такая, что для
каждого квадрата ABCD на плоскости f(A)+ f(B)+ f(C)+ f(D)= 0. Следует ли отсюда, что f(P) = 0 для всех точек P этой плоскости?
Задача 8: школьная
Дан прямоугольный треугольник, гипотенуза равна 10, высота проведённая к гипотенузе равна 6, найти площадь треугольника.
Задача 9:
Однокруговой баскетбольный турнир 2m команд продолжается 2m-1 день. Каждый день проводится m игр и каждая команда играет ровно одну игру. В итоге каждая сыграла ровно один раз. Всегда ли можно выбирать каждый день команду, победившую в этот день, так, чтобы все 2m-1 выбранных команд были различны?
Задача 10:
Есть старый автомобиль, которому надо сначала въехать на холм, а затем с него спуститься. Расстояние до вершины холма ровно одна миля, такой же длины и спуск. Общий путь соответственно две мили. Средняя скорость при подъеме автомобиля на холм — 15 миль/час. C какой скоростью должен ехать автомобиль с холма, чтобы средняя скорость движения на всем пути составила ровно 30 миль/час?
Задача 11:
Что это : 
?
Задача 12:
На плоскости заданы не лежащие на одной прямой точки K L, и M с целыми координатами так, что расстояния KL KМ , и
LМ являются целыми. Каково наименьшее возможное значение KL?
Задача 13:
решите уравнение корень квадратный из -x = x^3
Задача 14:
Для каких целых положительных чисел m найдется матрица размера m х m с целыми коэффициентами такая, что каждое скалярное произведение строки матрицы на себя является четным, в то время как каждое скалярное произведение двух различных строк является нечетным?
Задача 15:
пусть есть любое натуральное число K, если оно нечетное то действуем по правилу 3K+1, если четное то делим на 2.
К результату применяем те же правила. Докажите что рано или поздно получится 1.
Задача 16:
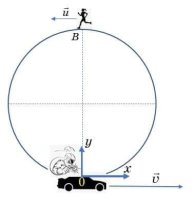
Вовочка в 8-ом классе все еще был оболтус оболтусом. Взял ключи от папиного автомобиля и ну гонять по круговой трассе диаметром 200 м со скоростью v = 72 км/ч. Девочки развиваются быстрее и Леночка из параллельного 8-Б класса была полностью сформировавшейся личностью. Она шла в кильватере лидера поколения Греты, прекрасно понимала, что автомобиль – зло и перемещалась в пространстве без использования углеводородов. В тот момент, когда Вовочка проезжал точку А, Леночка как раз в точке В бежала со скоростью u = 10 км/ч на семинар клуба Греты. С какой скоростью преодолевает пространство Леночка в системе отсчета, где автомобиль Вовочки покоится?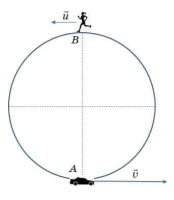
Задача 17:
Если поставить горящую свечу возле стены и включить горизонтальное освещение, то яркую тень отбрасывает только тело свечи и фитиль. А вот тень от пламени практически не видна. Хотя мы хорошо видим пламя, для человеческого глаза оно не является прозрачным. Почему же практически не видна тень от пламени ? Объясните с точки зрения физики процесса.
Отредактировано Stranger (, 2 года 7 месяцев назад)
dzen.ru/neuron
Дурак стал нормой, ещё немного - и дурак станет идеалом.
Учитывая глупость большинства людей, широко распространенная точка зрения будет скорее глупа, чем разумна.
